When you see two robotic arms seamlessly working together to fold clothes, pour tea, and pack shoes, coupled with the recent top-trending 1X humanoid robot NEO, you might get the feeling that we’re finally entering the robot age.
These smooth actions are the result of cutting-edge robotic technology combined with sophisticated framework design and multimodal large models. We recognize that useful robots often need to interact intricately with their environments, which can be represented by constraints in both spatial and temporal domains.
For example, to have a robot pour tea, the robot first needs to grasp the teapot handle and keep it upright so that no tea spills out. Then, it needs to ensure smooth movement to align the teapot spout with the cup and tilt the teapot at a certain angle. These constraints are not merely intermediate goals—like aligning the teapot spout with the cup—but also transitional states, such as keeping the teapot upright. They collectively dictate the robot’s actions in relation to its environment in terms of space, time, and other factors.
However, creating these constraints in the complex real world is a challenging problem.
Recently, Fei-Fei Li’s team made a significant breakthrough in this research direction by proposing Relational Keypoint Constraints (ReKep). Simply put, this method represents tasks as a sequence of relational keypoints and integrates seamlessly with multimodal large models like GPT-4. Their demonstration videos showcase impressive performance, and the team has released the relevant code. Wenlong Huang is the lead author of this work.

Fei-Fei Li noted that this work demonstrates a deeper integration of vision and robotic learning. While the paper does not mention Fei-Fei Li’s recently established AI company World Labs, which focuses on spatial intelligence, ReKep clearly has substantial potential in the realm of spatial intelligence.
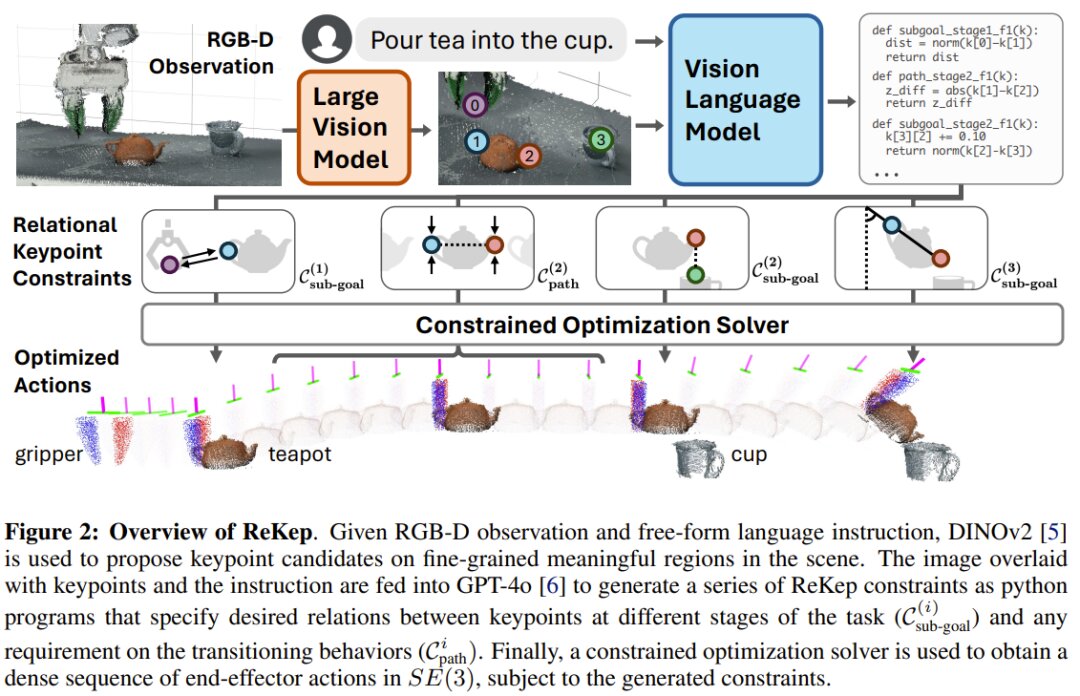
Overview of Relational Keypoint Constraints (ReKep)
Let’s delve into a ReKep instance. Assume we have a set of K keypoints, where each keypoint ( k_i \in ℝ^3 ) is a 3D point on the scene’s surface with Cartesian coordinates.
A ReKep instance is essentially a function ( f: ℝ^{K×3}→ℝ ). This function maps a set of keypoints (denoted as ( 𝒌 )) to an unbounded cost. The constraint is satisfied when ( f(𝒌) ≤ 0 ). For implementation, the team realized this function as a stateless Python function containing NumPy operations, which could be non-linear and non-convex. Essentially, a ReKep instance encodes a required spatial relationship among keypoints.
An operational task typically involves multiple spatial relationships and possibly several temporally-related stages, each requiring distinct spatial relationships. Therefore, the team decomposed a task into N stages, employing ReKep to specify two types of constraints for each stage ( i \in {1, …, N } ):
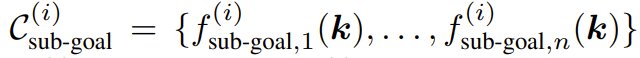
For illustration, let’s revisit the tea-pouring task, which consists of three stages: grasping, aligning, and pouring.
- Stage 1 sub-goal constraint is to reach for the teapot handle with the end-effector.
- Stage 2 sub-goal constraint is to align the teapot spout above the cup. Additionally, the Stage 2 path constraint is to keep the teapot upright to avoid spilling.
- The final Stage 3 sub-goal constraint is to achieve the specified pouring angle.
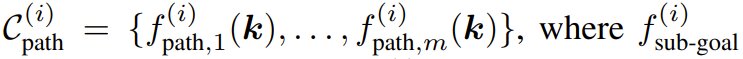
Using ReKep, the operational task is defined as a constraint optimization problem involving sub-goals and paths. The goal is to obtain the overall discrete-time trajectory ( 𝒆_{1:T} ):
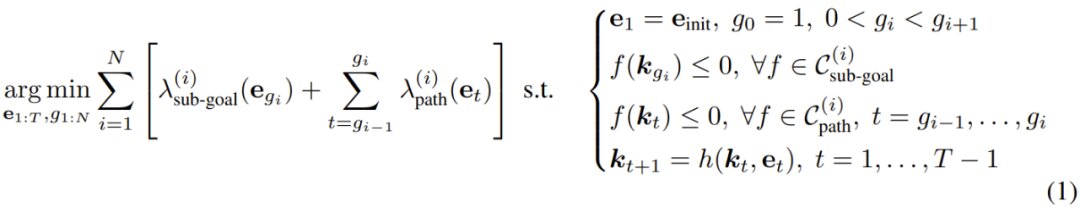
For each stage ( i ), the optimization objective is to identify an end-effector pose acting as the next sub-goal (and its relevant time) and the pose sequence to achieve this sub-goal. This formula can be perceived as direct shooting in trajectory optimization.
Decomposition and Algorithm Instantiation
To solve the above equation in real-time, the team adopted a decomposition approach, optimizing solely for the next sub-goal and the corresponding path to achieve it. Algorithm 1 presents this process in pseudocode.

Addressing Real-World Challenges
Given the dynamic and unpredictable real-world environment, re-planning is sometimes necessary if a prior stage’s sub-goal constraint fails (e.g., when the cup is removed while pouring tea). The team addressed this by checking for path discrepancies and iteratively backtracking to previous stages when issues arise.
Keypoint Forward Model
To solve the equations, the team utilized a forward model ( h ) that estimates ( ∆𝒌 ) based on ( ∆𝒆 ). Specifically, given the end-effector pose change, the model computes keypoint position changes by assuming other keypoints remain stationary.
Keypoint Proposals and ReKep Generation
To enable the system to perform varied tasks autonomously, the team incorporated a large model for keypoint proposal and ReKep generation. They used large visual models and visual-language models to design a pipeline for this purpose.
Keypoint Proposals
For an RGB image, they first used DINOv2 to extract patch-level features ( F{patch} ). These features were then upsampled using bilinear interpolation to match the original image size (( F{interp} )). They employed Segment Anything (SAM) to extract masks ( M = {m1, m2, … , m_n} ), covering all relevant objects in the scene. For each mask, they used k-means (k=5) with cosine similarity to cluster the features, and the centroids served as candidate keypoints, projected into world coordinates ( ℝ^3 ). Candidates within 8cm of each other were filtered out.
ReKep Generation
Once candidate keypoints were identified, they were overlaid on the original RGB image and numbered. Coupled with task-specific language instructions, GPT-4 was queried to generate the necessary sub-goal and path constraints for each stage.
Experimentation and Results
The team validated their constraint design framework through experiments aimed at answering three questions:
- How does the framework perform in automatically constructing and synthesizing operational behaviors?
- How well does the system generalize to new objects and operational strategies?
- What component failures might lead to system errors?
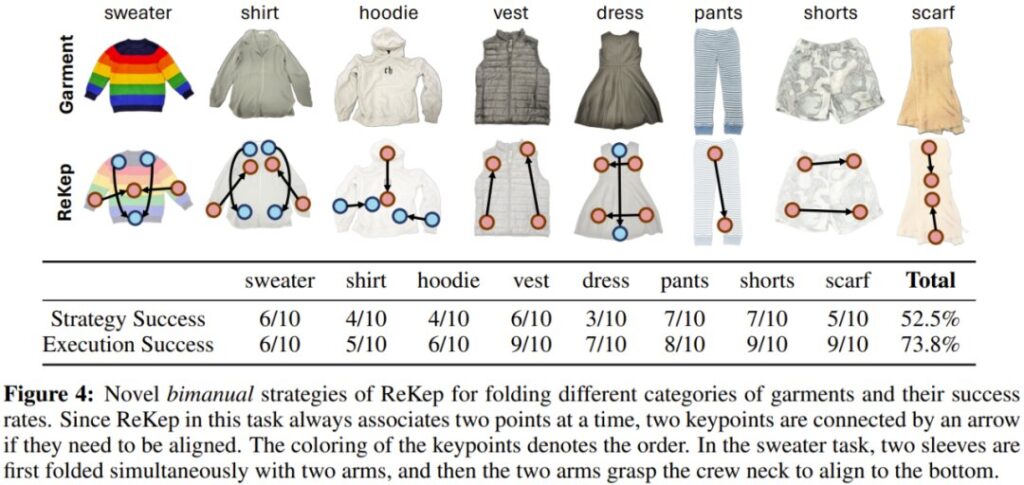
They tested the framework across various tasks to examine its multi-stage, field/practicality, bimanual, and reactive behaviors. Tasks included pouring tea, arranging books, recycling cans, taping boxes, folding clothes, packing shoes, and collaborative folding.
Results are shown in Table 1, depicting the success rates.
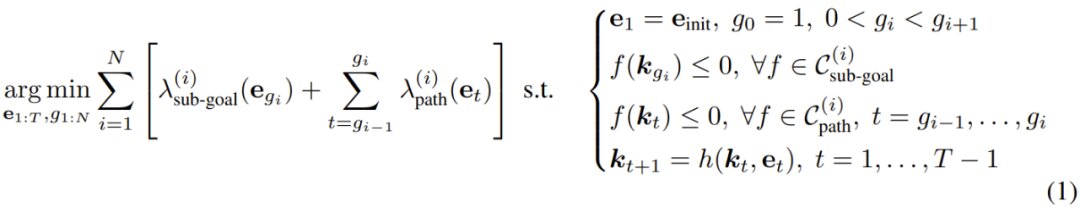
Generalization of Operational Strategies
The team explored the framework’s ability to generalize new strategies through a folding clothes task. This required reasoning both geometrically and commonsensically. They used GPT-4, providing it with general instructions without context-specific examples.

Analyzing System Errors
The framework’s modular design facilitated error analysis. They manually inspected failure cases to compute the likelihood of errors originating from different modules, considering their temporal dependencies within the pipeline.
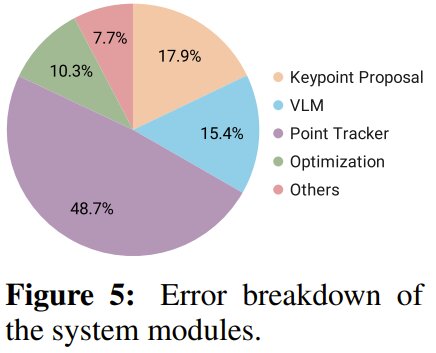
The findings indicate that errors frequently stemmed from the keypoint tracker, primarily due to regular and intermittent occlusions hampering accurate tracking.